Geometric Brownian Motion

import numpy as np
import pandas as pd
import plotly.express as px

Theory

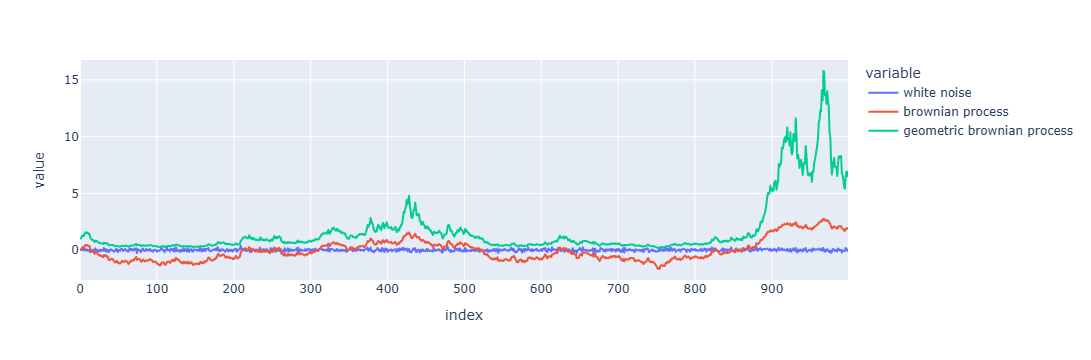
A Brownian process (or “random walk”) \(B_t\) is such that \[ \nabla B_t \sim \mathcal N(0, \sigma^2) \] If we exponentiate it, we get a geometric Brownian process, \(S_t\). In other words, \(S_t\) is such that \[ \nabla \ln(S_t) \sim \mathcal N(0, \sigma^2) \]

Synthetic Data and Visualization

ran = np.random.RandomState(seed=42)

white_noise = ran.normal(0, 0.1, 1000)
df = pd.DataFrame(white_noise, columns=['white noise'])

df['brownian process'] = df['white noise'].cumsum()

df['geometric brownian process'] = np.exp(df['brownian process'])

px.line(df)