import warnings
warnings.filterwarnings("ignore")

1. Theory

One of the central concepts of Data Science and related disciplines is that of loss function: a function \(f(\theta)\), whose minimization provides the “best value” for the parameters \(\theta\) of the model. Arguably, the simplest example is that of mean square error, commonly used for regression problems: \[ f(\theta) = \dfrac{1}{N} \sum_i \left[y_i - M_\theta(x_i)\right]^2 \] where the sum is over all \(N\) samples in the dataset, \(x_i\) and \(y_i\) are the feature vector and the target scalar of sample \(i\) respectively, and \(M_\theta: x \to y\) is the model.

But where do these loss functions come from? Enter the concept of likelihood!

Let’s start by noting that the dataset \(D := \{(x_i, y_i)\}_i\) can be seen as \(N\) independent observations of the random variable \(Y|X\), whose probability density we denote by \(p_{Y|X}\). By definition, the model \(M_\theta\) should produce the expected value of this variable: \[ M_\theta(x) = \mathbb E[Y|X=x] \]

A common (and reasonable) assumption for a variable \(Y\) whose possible values are in \(\mathbb R\), is that \[ Y|X \sim \mathcal N(\mu(X), \sigma(X)^2) \] In this case, \(M_\theta(x) = \mathbb E[Y|X=x] = \mu(x)\), and if we assume that \(\sigma(x) = \sigma\) is a constant, then \[ p_{Y|X}(y|x, \theta) = \dfrac{1}{\sqrt{2\pi \sigma^2}} \exp\left[-\dfrac{1}{2\sigma^2} (y - M_\theta(x))^2\right] \] where we made explicit the dependence on \(\theta\).

It follows that, given the model with parameters \(\theta\), the probability of observing the dataset \(D\) is \[ P(D|\theta) = \prod_i p_{Y|X}(y_i|x_i, \theta) = \left(\dfrac{1}{2\pi \sigma^2}\right)^{\frac{N}{2}} \exp\left[-\dfrac{1}{2\sigma^2} \sum_i (y_i - M_\theta(x_i))^2\right] \] Seen as a function of \(\theta\), this quantity represents the “likelihood” that the data \(D\) would be generated by model \(M_\theta\). Hence, the best values for parameters \(\theta\) will be those for which the probability \(P(D|\theta)\) is maximal: we thus talk about maximum likelihood estimation (MLE).

In fact, maximizing the likelihood is equivalent to maximizing the log-likelihood, \(\ell(\theta)\), which reads \[ \ell(\theta) := \ln(P(D|\theta)) = -\frac{N}{2} \ln(\sigma^2) - \dfrac{1}{2\sigma^2} \sum_i [y_i - M_\theta(x_i)]^2 \] up to a constant. It is now evident that \(\max_\theta \ell(\theta)\) coincides with \(\min_\theta f(\theta)\), with \(f\) the mean square error loss function defined above.

1.1 Binary Classification Case

We saw how the mean square error loss function typical of regression problems arises as the (negative) log-likelihood of data \(D := \{(x_i, y_i)\}_i\) when we think of \(y_1, ..., y_N\) as independent observations of random variable \(Y\) which, conditional to \(X\), follows a normal distribution.

Another common Data Science area is that of classification problems. For a binary classification, \(Y\) can only take values \(0\) or \(1\), and so we must have \[ Y|X \sim \text{Bernoulli}(\phi(X)) \] In this case, \(M_\theta(x) = \mathbb E[Y|X=x] = \phi(x)\), so \[ p_{Y|X}(y|x, \theta) = M_\theta(x)^y \ (1 - M_\theta(x))^{1 - y} \] It follows that the log-likelihood is \[ \ell(\theta) = \ln(P(D|\theta)) = \sum_i \ln(p_{Y|X}(y_i|x_i, \theta)) = \sum_i \left[y_i \ln(M_\theta(x_i)) + (1 - y_i) \ln(1 - M_\theta(x_i))\right] \] which we can recognise as the cross-entropy loss function (up to a sign), thus explaining why this is the usual loss function for binary classifiers.

2. Example

Let’s stay on binary classification, and see how maximum likelihood estimation (MLE) works in an example.

First, let’s generate some data based on Bernoulli distribution with \(M_\theta\) a sigmoid model with a single feature: \[ M_\theta(x) = \dfrac{1}{1 + e^{-\theta x}} \] To achieve this, we first generate \(N\) observations \(x_1, ..., x_N\) of the input variable \(X\) (here, without loss of generality, we take it to be normally distributed). We then determine the probabilities \(\phi_1, ..., \phi_N\) by the sigmoid \(\phi_i = \phi(x_i) = M_\theta(x_i) = 1/(1 + \exp(-\theta x_i))\). Finally, we generate \(N\) observations \(y_1, ..., y_N\) of the target variable \(Y\) via \(y_i \sim \text{Bernoulli}(\phi_i)\).

import numpy as np
import pandas as pd
import plotly.express as px

ran = np.random.RandomState(seed=42)

num_samples = 10000
theta_true = -1.2

def sigmoid(theta, x):
    return 1/(1 + np.exp(-theta * x))

# generate input data
x_data = ran.normal(0, 1, num_samples)

# compute probabilities phi's (phi_i denotes the probability that y_i = 1)
phi_s = sigmoid(theta_true, x_data)

# generate output data
y_data = np.array([1 if ran.uniform(0, 1) < phi else 0 for phi in phi_s])

# combine input and output in a dataframe
data = pd.DataFrame([x_data, y_data]).T
data.columns = ['x', 'y']

Let’s make a scatter plot of \(x\) vs \(y\):

fig = px.scatter(data, x='x', y='y')
fig.show()

Suppose we knew that this data comes from a sigmoid model, but we did not know the true value of parameter \(\theta\). We can see by naked eye that the true value must be negative, since samples with higher \(x\) tend to have decreased probability that \(y=1\). But to find the correct value of \(\theta\) we must ask: What is the value of \(\theta\) for which the data above is most likely? In other words, we look for the \(\theta\) that maximizes the (log) likelihood.

Let’s therefore plot this function for a range of values of \(\theta\).

def log_likelihood(theta):
    y_pred = sigmoid(theta, x_data)
    return np.sum(y_data * np.log(y_pred) + (1 - y_data) * np.log(1 - y_pred))

theta_vals = np.linspace(-6, 6, 1000)
ll_vals = [log_likelihood(theta) for theta in theta_vals]

output = pd.DataFrame([theta_vals, ll_vals]).T
output.columns = ['theta', 'log-likelihood']

fig = px.line(output, x='theta', y='log-likelihood')
fig.show()

We see that the log-likelihood has a maximum around 1. To identify the exaclt value, we could implement a gradient ascent algorithm and use it to maximize the log-likelihood – but python already thought about that, and it provides a library to minimize a given function: this is the reason why, in the code, we always use the negative log-likelihood.

from scipy.optimize import minimize

def neg_log_likelihood(theta):
    return -log_likelihood(theta)

result = minimize(neg_log_likelihood, x0=0.0) # x0 is the initial guess

theta_estimated = result.x[0]
print(f"Estimated theta: {theta_estimated:.2f}")
print(f"True theta: {theta_true:.2f}")

Estimated theta: -1.19
True theta: -1.20

Our estimation is very close to the true value we generated the data with: the MLE approach worked!

3. Application: Simple Price Simulations

Let’s now investigate some more realistic application of MLE. We will consider the daily price time series of a stock (in this case, Nvidia). Our purpose is to define a simple model for this time series, a model based on a few parameters. We will then use MLE to estimate such parameters, and finally generate some future possible paths according to the model.

First, load the data and visualize it.

# load data

df = pd.read_csv('data/likelihood-1.csv', parse_dates=['date']).set_index('date')
price = df['price']

# visualize

fig = px.line(price, y='price')
fig.show()

# compute auto-correlation and partial auto-correlation funcitons

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt

fig, axes = plt.subplots(1, 2, figsize=(14, 5))

plot_acf(price, lags=30, ax=axes[0])
axes[0].set_title('Autocorrelation Function')
axes[0].set_xlabel('Lag')

plot_pacf(price, lags=40, ax=axes[1])
axes[1].set_title('Partial Autocorrelation Function')
axes[1].set_xlabel('Lag')

plt.tight_layout()
plt.show()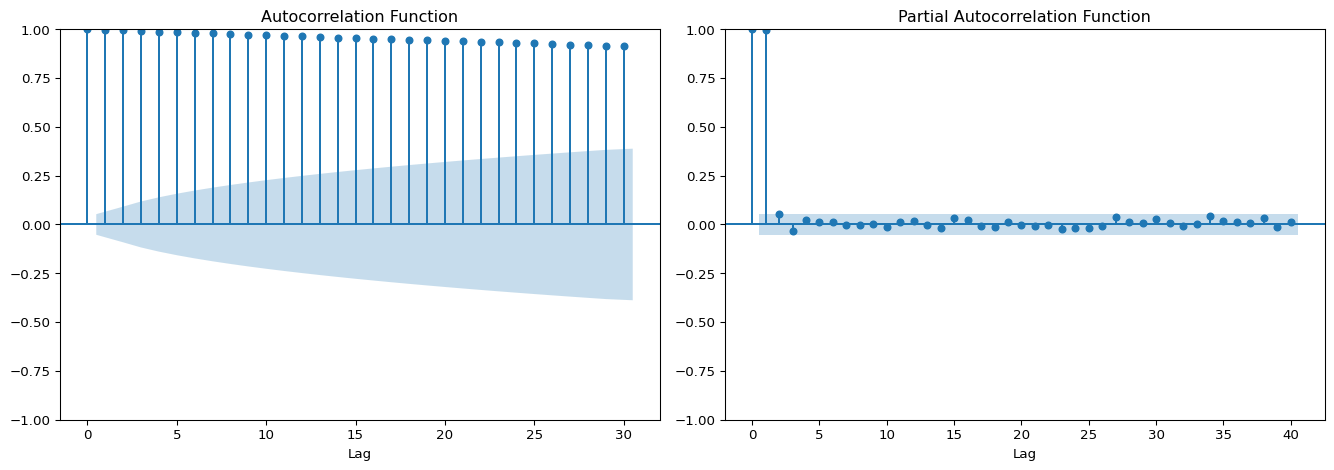

As it is usual for prices, the series presents a strong 1-lag autocorrelation. This suggests modelling the return: \[ R_t := \nabla P_t = P_t - P_{t-1} \]

R = df['price'].diff(1)

fig = px.line(R)
fig.update_layout(yaxis_title='return', showlegend=False)
fig.show()

The series \(R_t\) suffers from heteroscedasticity, meaning that the standard deviation is not constant in time. A simple solution is to consider the rate of return: \[ r_t := \dfrac{P_t - P_{t-1}}{P_{t-1}} \approx \nabla_t \ln(P_t) \]

r = np.log(df['price']).diff(1)

fig = px.line(r)
fig.update_layout(yaxis_title='rate of return', showlegend=False)
fig.show()

Not only does this makes the series homoscedastic, but it also means that, modelling \(r_t\), we ensure our forecasted prices will never be negative, since \[ \hat P_{t+1} := P_t \exp(\hat r_{t+1}) \]

The simplest model for \(r_t\) is that of a normal random variable: \[ r_t \sim \mathcal N(\mu_o, \sigma_o^2) \] This is equivalent to say that \(P_t\) follows as a geometric Brownian process with drift, whose stochastic differential equation reads \[ dP_t = P_t (\mu_o dt + \sigma_o dB_t) \] where \(B_t\) is a Brownian process, and drift \(\mu_o\) and volatility \(\sigma_o\) are constants.

Given that \(r_t \sim \mathcal N(\mu_o, \sigma_o^2)\), we could find parameters \(\mu_o\) and \(\sigma_o\) by simply computing the mean and the standard deviation of the time series \(r_t\). However, to see MLE in its glory, we follow a different route.

First, we discretize the stochastic differential equation: \[ P_{t+\Delta t} - P_t = P_t (\mu_o \Delta t + \sigma_o \epsilon_{t+\Delta t}) \] where we used the Brownian process property that \(B_{t+\Delta t} - B_{t} \sim \mathcal N(0, \Delta t)\) to replace the discretization of \(dB_t\) with \(\epsilon_{t+\Delta t} \sim \mathcal N(0, \Delta t)\). If we set \(\Delta t = 1\) (meaning that we’ll have to remember that the parameters are relative to 1-day time step), then the equation simplifies to \[ P_{t+1} = (1 + \mu_o) P_t + \sigma_o P_t Z_{t+1} \] where \(Z_t \sim \mathcal N(0, 1)\). This is equivalent to \[ P_t|P_{t-1} \sim \mathcal N(\mu(P_{t-1}), \sigma(P_{t-1})^2) \] where \[ \mu(P_{t-1}) := (1 + \mu_o) P_{t-1}, \ \ \ \ \ \sigma(P_{t-1}) = \sigma_o P_{t-1} \] If we think of \(P_t\) as the observation \(y_t\) of target variable \(Y\) and as \(P_{t-1}\) as the observation \(x_t\) of input feature(s) \(X\), we see that this system is a special case of the formula from above: \[ Y|X \sim \mathcal N(\mu(X), \sigma(X)^2) \] with the difference that now \(\sigma(X)\) is not constant, as it clearly depends on \(X_t = P_{t-1}\).

The likelihood of observations \(P_1, ..., P_T\) is \[\begin{align} P(D|\mu_o, \sigma_o) & = \prod_{t=1}^T p(Y_t|X_t, \mu_o, \sigma_o) = \prod_{t=1}^T \dfrac{1}{\sqrt{2\pi \sigma(X_t)^2}} \exp\left(-\dfrac{(Y_t - \mu(X_t))^2}{2\sigma(X_t)^2}\right) \\ \\ & = \prod_{t=1}^T \dfrac{1}{\sqrt{2\pi \sigma(P_{t-1})^2}} \exp\left(-\dfrac{(P_t - \mu(P_{t-1}))^2}{2\sigma(P_{t-1})^2}\right) \end{align}\]

Let’s write code to compute the value of the negative log-likelihood given as inputs the parameters \(\mu_o\) and \(\sigma_o\).

def mu_model(mu0, x):
    return (1 + mu0) * x

def sigma_model(sigma0, x):
    return sigma0 * x

def neg_log_likelihood(params, price):
    
    mu0, sigma0 = params
    if sigma0 <= 0: # ensure sigma0 > 0
        return np.inf

    # build the data, consisting of target y = P and of input X (P at t-1)
    data = pd.DataFrame()
    data['P_t'] = price
    data['P_t-1'] = price.shift(1)
    data = data.dropna()

    # separate target from input
    x = data['P_t-1']
    y = data['P_t']
    
    # compute mu(X) and sigma(X) 
    mu = mu_model(mu0, x)
    sigma = sigma_model(sigma0, x)

    # negative log-likelihood for normal distribution
    nll = 0.5 * (np.log(sigma**2) + ((y - mu) ** 2) / sigma**2).sum()
    
    return nll

Now we can estimate the parameters by minimizing the negative log-likelihood.

def estimate_params(df):

    price = df['price']

    # initial guess
    mu0_init = 0
    sigma0_init = 0.01

    # minimize negative log-likelihood
    result = minimize(neg_log_likelihood, x0=(mu0_init, sigma0_init), args=(price))

    mu0, sigma0 = result.x
    return mu0, sigma0

mu0_estim, sigma0_estim = estimate_params(df)

print(f"NLL with initial guess: {neg_log_likelihood((0, 0.02), price):.2f}")
print(f"NLL with estimated parameters: {neg_log_likelihood((mu0_estim, sigma0_estim), price):.2f}")

print(f"\nParameters estimated via MLE:")
print(f"mu0 = {mu0_estim:.4f}")
print(f"sigma0 = {sigma0_estim:.4f}")

NLL with initial guess: 1330.40
NLL with estimated parameters: 709.95

Parameters estimated via MLE:
mu0 = 0.0029
sigma0 = 0.0345

We see that the negative log-likelihood is indeed lower when evaluated on the estimated parameters than when evaluated on the initial guess: a good indication that our minimization algorithm was successful.

Having identified the best parameters, we can use them to simulate several possible future paths that the price might take.

def simulate_paths(x0, mu0, sigma0, T=100, N=100, seed=None):

    ran = np.random.RandomState(seed=seed)
    
    paths = np.zeros((N, T + 1))
    paths[:, 0] = x0

    for t in range(1, T + 1):

        x = paths[:, t-1]

        mu = mu_model(mu0, x)
        sigma = sigma_model(sigma0, x)
        
        paths[:, t] = ran.normal(mu, sigma)

    paths = pd.DataFrame(paths[:, 1:]).T
    return paths

periods = 250
simulations = 10

historical_price = df['price']
last_price = historical_price.iloc[-1]
paths = simulate_paths(last_price, mu0_estim, sigma0_estim, T=periods, N=simulations, seed=123)

start = df.index[-1] + pd.Timedelta(days=1)
index = pd.date_range(start=start, periods=periods, freq='D')
paths.index = index

historical_price_df = pd.concat([historical_price] * paths.shape[1], axis=1)
historical_price_df.columns = paths.columns
paths = pd.concat((historical_price_df, paths), axis=0)
paths.index.name = 'date'

fig = px.line(paths)
fig.update_layout(yaxis_title='price', legend_title_text='simulations')
fig.show()

Our model seems to be quite optimistic on the future of Nvidia… Perhaps it’s still a bit too simple!

To conclude, it is interesting to compare the parameters we estimated via MLE with those we would find by simply computing the mean and standard deviation of the rate of return \(r_t\).

print(f"\nParameters computed from r:")
print(f"mu0 = {r.mean():.4f}")
print(f"sigma0 = {r.std():.4f}")


Parameters computed from r:
mu0 = 0.0023
sigma0 = 0.0343

Given that this simpler method produces essentially the same results, one might wonder why we went through the trouble of performing MLE.

The answer is that the MLE method allows much more general models. For example, the input \(X_t\) of functions \(\mu(X_t)\) and \(\sigma(X_t)\) could be a vector (not just the scalar \(P_{t-1}\)), consisting of many autoregressive and seasonal components, as well as calendar features and other fundamental drivers. Moreover, the functions \(\mu\) and \(\sigma\) themsleves need not be linear in the parameters: we might want to consider more complex relations. In fact, we might even keep them as “black boxes” by modelling them via neural networks, letting the algorithm “learn” what the drift and the volatility should be in terms of inputs \(X_t\)… But this is a topic for a future post!